Intelligence explicable avec les outils du Web sémantique - Partie 1
Posté le 15/12/2022 par Anabasis
Traductions: enCatégories: Technologie
L’intelligence artificielle explicable est l’un des fondements des solutions développées par Anabasis. Comme toutes techniques d’intelligence artificielle (IA), l’IA explicable cherche à simuler par une machine l’intelligence humaine (que l’on comprendra ici comme la capacité à raisonner pour aboutir à une conclusion). Si d’autres techniques reposent sur une métaphore machine du support physique de cette intelligence, le cerveau, avec par exemple les réseaux de neurones artificiels et tous ses dérivés, l’IA explicable se concentre sur les mécanismes abstraits du raisonnement, leur mathématisation avec la logique formelle, et leurs mises en œuvre par des machines. Son caractère explicable provient de ses racines logiques garantissant la justesse de ses conclusions et leur fiabilité.
Ce type d’IA a été proposé très tôt avec l'apparition des systèmes experts vers la fin des années 1960 suivie d'une forte explosion dans les années 1970. On pourrait évoquer par exemple le projet MYCIN qui débuta en 1972. Un système expert est un outil qui a vocation à se substituer à un spécialiste d'un domaine d'expertise. Les systèmes experts à base de règles permettent d’exprimer un problème en termes logiques : à partir d’un ensemble de vérités initiales (faits) et de règles logiques (savoirs métier), le système infère les nouvelles connaissances déductibles dans l’objectif de résoudre le problème. Ces systèmes se sont offert une nouvelle jeunesse dans le début des années 2000 avec l’avènement du web sémantique, terme que l'on doit notamment à Tim Berners-Lee, dont l’objectif est d'ajouter aux pages web traditionnelles à destination des internautes, des sources de données structurées à destination des machines. Cette renaissance s’est accompagnée de la définition de nouveaux standards dont le lecteur aura sûrement déjà croisé certains acronymes : RDF, RDFS, OWL, SPARQL, SWRL, RIF, etc.
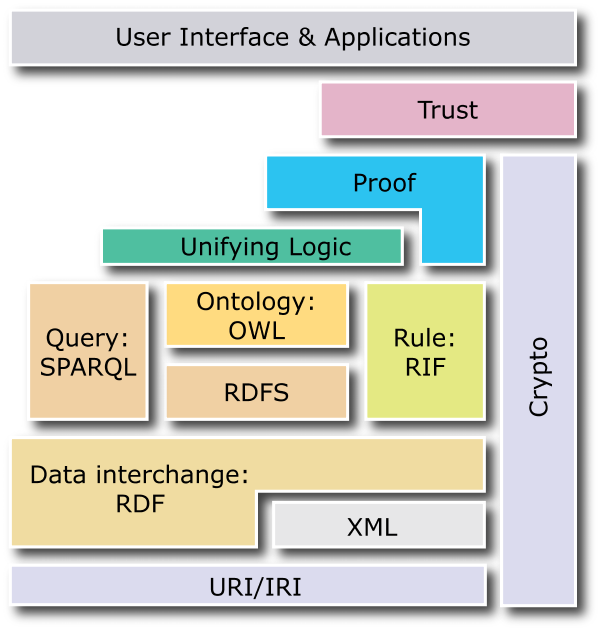
Nous vous proposons une série de quelques billets pour décrire cet univers et comment ces technologies de l’intelligence artificielle permettent de basculer de systèmes d'information classiques à des systèmes d'information intelligents. Nous aborderons les idées générales avec quelques incursions techniques en illustration. Pour satisfaire la curiosité des personnes voulant aller plus loin, les liens importants seront mentionnés. Pour ce premier volet, nous allons parler des graphes de connaissances et de leur utilisation comme modèle de base de données.
Des connaissances et des graphes
Bien que le buzz word du moment soit la data, ce qui intéresse réellement est la capacité d'en récupérer de l'information, des connaissances. Si l'on évacue (d'un revers de main un peu facile on le concède) la problématique de l'analyse de données, il reste la question de la représentation en vue d'une exploitation des connaissances acquises.
La représentation des connaissances est le domaine dans lequel on cherche à développer des outils permettant la communication, le partage d’un ensemble de connaissances. Ces outils sont de natures très variées car ce domaine ne concerne pas uniquement l'informatique ; les dessins, les plans, les cartes, les taxonomies, classifications, thésaurus et autres mind maps, sont autant de propositions entrant dans le cadre de la représentation de connaissances. Nous allons nous concentrer sur des représentations formalisées, donc accessibles aux machines, comme les réseaux sémantiques [A] ou les graphes conceptuels [B,C]. Plus particulièrement, nous allons parler de graphes de connaissances.
L’idée fondatrice des graphes de connaissances est d’utiliser un graphe pour véhiculer du savoir. Mathématiquement parlant, il existe beaucoup de sortes de graphes : multi-graphes, hyper-graphes, graphes dirigés ou non dirigés, graphes acycliques, arbres, forêts, … On fait un peu ce qu'on veut. Cependant, toutes ces sortes ont en commun qu'un graphe est en gros constitué d'une collection de nœuds et de liens entre ces nœuds. Pour ce qui des graphes de connaissances, étant donné un univers que l'on souhaite représenter (des savoirs métier, des modélisations de systèmes, les personnages de la famille Simpson, etc.), les nœuds seront des abstractions des atomes de cet univers et les flèches entre paires de nœuds incarneront des relations sémantiques existantes entre ces différents atomes. Voici un exemple :
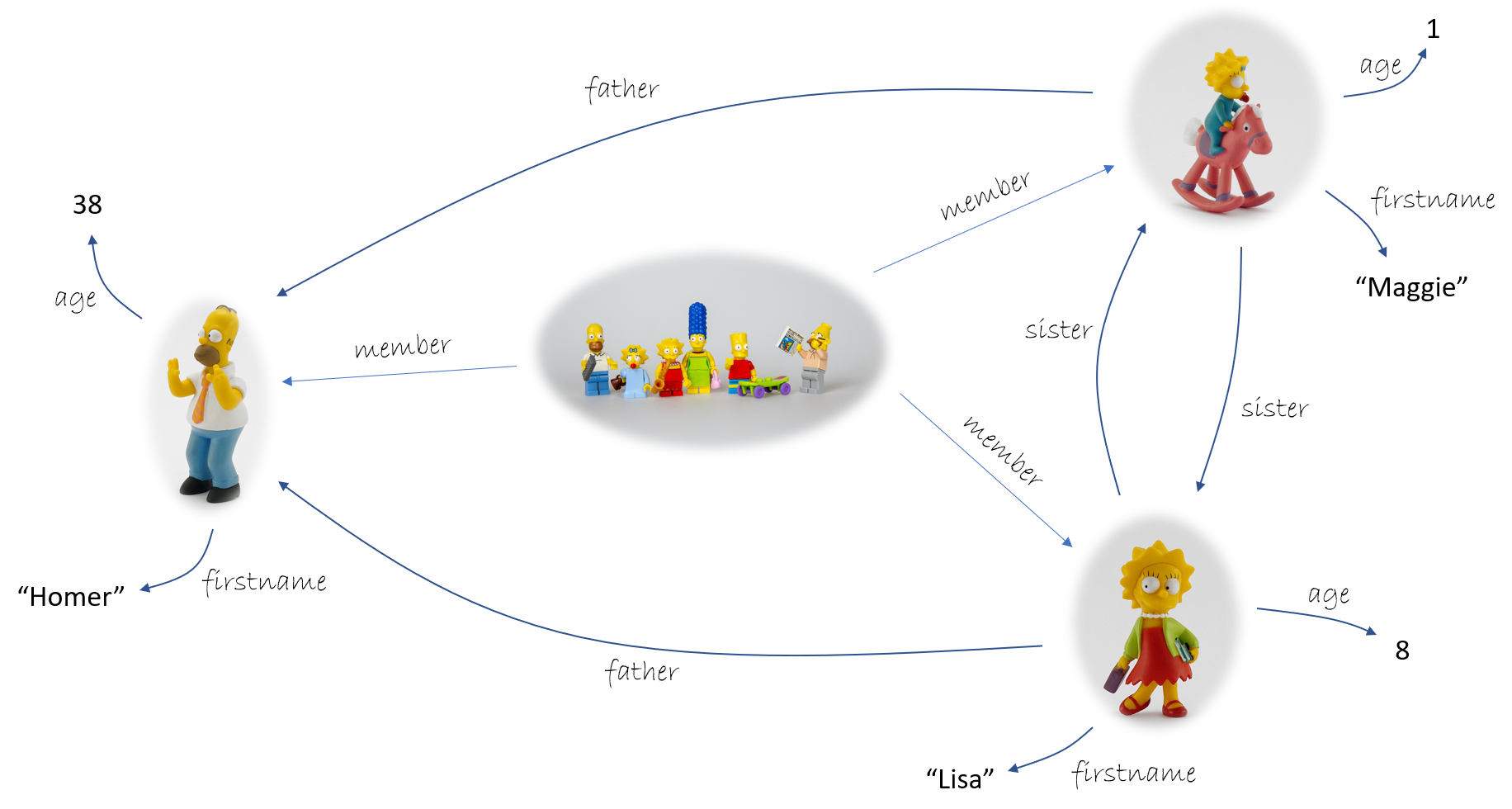
Des triplets chez les Simpson
Parmi les nombreuses structures de données permettant d'attraper ces graphes de connaissances, l'une d'elles consiste à utiliser l'arc comme l'élément constitutif primordial. Ce point de vue est celui promu par le standard RDF. Le graphe est construit comme une collection d'arcs appelés triplets, chacun de la forme
< sujet prédicat objet >
et décrivant un arc allant d'un nœud sujet à un nœud objet, et décoré par la relation entre ces nœuds appelée prédicat. Voici quelques triplets tirés de la représentation graphique précédente :
< lisa firstname "Lisa" >
< lisa sister maggy >
< maggy age 1 >
< maggy father homer >
…
Cette représentation a pour avantage sa simplicité et son homogénéité mais mène tout de même à quelques observations pratiques :
- Retrouver les nœuds : si le graphe est défini à travers ses arcs, la première question que l'on se pose est celle de retrouver les nœuds. Pour y répondre, il nous faut évoquer la nature des éléments composant les triplets. Très clairement, ces éléments permettent de faire référence à la source et à la destination de chaque arc, et donc aux nœuds du graphes. Plus précisément, ils permettent de distinguer les nœuds entre eux et les arcs entre chaque paire de nœuds. Il s'agit donc d'identifiants. L'utilisation d'un même identifiant fait ainsi référence au même atome de connaissance représenté. On pourra alors demander l'ensemble des arcs sortants d'un nœud donné (i.e., tous les triplets ayant un certain identifiant en sujet) ou toutes les pairs de nœuds mis en relation par le même prédicat (i.e., tous les triplets ayant comme élément central un identifiant donné). Il existe des langages pour requêter de cette façon les graphes de connaissances et l'on pointera plus particulièrement SPARQL dans le cadre de RDF.
- Portée symbolique des identifiants : il est important de reconnaître la portée purement symbolique, donc non-informative, des identifiants. En effet, la capacité de représentation d'un graphe de connaissances se limite à sa structure. Dit d'une autre façon, renommer les nœuds et les arcs ne change pas le contenu informatif du graphe. Ainsi, on pourrait tout à fait choisir le renommage suivant pour notre exemple :
< person1 firstname "Lisa" >
< person1 sister person2 >
< person2 age 1 >
< person2 father person3 >
…
Aussi, la présence d'un nœud person4 sans aucun lien dans le graphe ne nous apporte aucune information supplémentaire (ni même qu'il s'agit effectivement d'une personne !). Cela n'empêche pas de choisir astucieusement les identifiants utilisés, mais la portée informative du choix d'un symbole plutôt qu'un autre sort du champ des connaissances représenté par le graphe à proprement parler.
- Quelques limitations : l'utilisation des triplets et des identifiants pour représenter un graphe entraîne certaines limitations. Elle empêche par exemple de pouvoir considérer des nœuds isolés, c'est-à-dire des nœuds n'étant ni source, ni destination d'aucun arc. Comme nous venons de le voir, cette limitation n'enlève pas réellement d'expressivité dans le contexte de la représentation de connaissances, sauf à vouloir questionner la présence ou l'absence d'un nœud particulier. De même, deux arcs entre deux nœuds donnés ne peuvent pas être décorés par le même identifiant, sans quoi, les triplets les représentant ne sauraient être distingués. Ces limitations ne sont ni bonnes ni mauvaises mais plutôt opportunes ou non selon les circonstances. Comme pour tous les systèmes, il y a des limites et il s'agit simplement de savoir qu'elles existent.
- Les data et object properties : en regardant notre exemple, une incohérence semble apparaître : l'objet du triplet
< homer age 38 >semble être bien plus qu'un identifiant renommable. En effet, le nœud38vient avec une sémantique précise. Ces nœuds particuliers correspondent à des valeurs littérales, également appelées constantes. Venant avec leur propre sémantique (à travers un standard, par exemple les types de données primitives en XML Schema), les constantes ne sont pas autorisées à être décrites dans le graphe ; on retrouve le fait que le symbole fait référence à une connaissance extérieure à l'univers attrapé par la structure du graphe (ouf… finalement, pas d'incohérence). Cela se traduit par des nœuds ne pouvant pas apparaître en sujet de triplet.
Plus précisément, on distingue deux types de nœuds : les constantes et les nœuds objets. Les premiers ne peuvent être utilisés qu'en troisième position dans les triplets. Ces triplets décrivent ce que l'on appelle une data property du nœud sujet. Les autres nœuds (comme lisa, maggy et homer) ont une portée informative différente dans le sens où ils font référence à des éléments forts de l'univers de connaissances représenté. Les triplets les ayant en troisième position spécifient ce que l'on appelle une object property du nœud sujet ; ils sont essentiels car ils constituent le tissu de la structure réelle des connaissances modélisées.
Les vieilles habitudes ne sont jamais très loin…
Les graphes de connaissances fournissent un modèle de données et une base de données mettant en œuvre ce modèle est appelée triplestore. C'est sur ce type de système que nous allons raisonner comme nous le verrons dans le billet suivant. Mais avant de passer à ces autres volets, voyons comment plonger une base de données plus traditionnelle dans un triplestore. On entend par traditionnel le modèle relationnel qui invite à ranger les données dans des tables, ou relations, comme la suivante :
| firstname | age | father |
|---|---|---|
| Lisa | 8 | Homer |
| Maggy | 1 | Homer |
| Homer | 38 | Abraham |
| … | … | … |
Chaque tuple/ligne d'une telle table représente une entrée qui est décrite par la réponse à différentes questions données en colonne/attribut. Ainsi, toutes les entrées d'une même table sont décrites de la même façon. Dans ce modèle, deux lignes répondant de la même façon à toutes les questions ne sont pas distinguables. On forcera cette distinction par la présence d'un ou plusieurs attributs pour lesquels les réponses seront forcément différentes entre deux entrées. On appelle clé primaire cet ensemble d'attributs. La clé primaire joue le rôle d'identifiant et permet de faire des références entre les tuples. Ce mécanisme est appelé contrainte référentielle. Dans notre exemple, en considérant l'attribut firstname comme clé primaire, l'attribut father permet à chaque tuple de faire référence à une autre entrée de la table pour désigner son père.
La traduction vers un graphe de connaissances est assez directe : chaque tuple/ligne donne lieu à la création d'un nœud dans le graphe, et chaque attribut/colonne à un prédicat particulier. Ainsi les cases seront chacune traduite en un triplet de type data property dont le sujet sera le nœud associé au tuple, le prédicat sera celui associé à l'attribut, et l'objet sera le contenu de la case. La difficulté, s'il en est une, consiste à traduire les contraintes référentielles en object properties. Ainsi, l'attribut father précédent fait en fait référence à une autre ligne de la table (clé étrangère) ; ces références seront traduites comme des triplets dont l'objet sera l'identifiant du tuple référé.
::: info Cette traduction met en avant une différence fondamentale entre les deux approches : là où l'on choisit de nommer les objets représentés dans les graphes de connaissances, le modèle relationnel invite à identifier ces objets par leurs propriétés à travers le concept de clé primaire. Les conséquences non-négligeables de cette différence pourraient faire l'objet d'un billet à elles seules…
:::
Conclusion
Cette première partie a été consacrée à la description de l'une des pierres angulaires des technologies de l'intelligence artificielle explicable et des solutions Anabasis : les graphes de connaissances. Ils proposent un modèle de données simple et homogène permettant une exploitation systématique et de haut niveau de vos données. Nous avons également vu comment d'autres technologies existantes peuvent être plongées aisément dans le monde de la représentation de données à l'aide de graphes.
La présentation proposée dans ce billet est fortement orientée (à dessein) vers RDF. Si vous souhaitez plus d'informations sur le sujet, nous vous invitons à vous intéresser aux modèles de données orientés graphes dont font partie les graphes de connaissances à la RDF. On pourra en particulier citer les property graphs (par exemple chez Oracle ou neo4j) qui, à l'inverse des graphes de connaissances RDF, permettent de décorer les nœuds et les arcs avec des attributs. Une comparaison entre les deux modèles est disponible ici.
Antoine, expert scientifique
et
Clément, directeur technique
Références
- [A] W.A. Woods, What's in a Link: Foundations for Semantic Networks, Bolt, Beranek and Newman, 1975
- [B] Chein, M., & Mugnier, M. (1992). Conceptual graphs: fundamental notions.
- [C] Sowa, J.F. (1983). Conceptual Structures: Information Processing in Mind and Machine.
- https://www.w3.org/2001/sw/
- https://www.w3.org/2001/sw/wiki/
Mots clés : graphes de connaissances, représentation de connaissances, RDF, triplestore, web sémantique
L’IA explicable dans tous ses états (ou presque !) : quelques cas d’application
2024 marque un tournant pour Anabasis : après de belles mises en production chez des clients clés, nous avions besoin de prendre un peu de recul, au-delà des applications sectorielles ou métie
Intelligence explicable avec les outils du Web sémantique - Partie 2
Dans le billet précédent, nous nous sommes concentrés sur les graphes de connaissances à la RDF, à
Retour sur la participation d'Anabasis à SemWeb.Pro 2023
Parce qu'Anabasis Assets a construit sa suite logicielle sur les normes et standards du web sémantique (entre autres), il était naturel de participer à la Jou
