Blog

In the previous post, we focused on RDF-style knowledge graphs, the basis of Anabasis technologies. Now we are continuing with data schemas, which, in a nutshell, describe the organisation of knowledge graphs.

Ordered Chaos

The use of the unique concept of triplet to represent information makes knowledge graphs very homogeneous in their handling. It also makes them very flexible, maybe too flexible... The data model in fact suffers from the defect of its advantages. On the one hand, it allows a freedom of the representation where the data is directly related without any description prerequisites (compared with the tables of relational models that have to be defined in advance, for example). On the other hand, the absence of a framework means that anything and everything can be done. However, this disorder is only apparent. In practical terms, using a knowledge graph requires a certain amount of regularity in the representation in order to be able to process the data, or even just to understand the logic behind it.

Like other semi-structured data models (XML, JSON, etc.), knowledge graphs can be provided with a data schema, i.e. a sort of contract that the graph structure must comply with. The schema then has two roles: (1) describing the organisation of the data in the graph and therefore enable it to be used, but also (2) validating the structure of the given graph with a view to its use.

Schema and Modeling

Our aim is to understand the value of the schema in the context of modeling, where the data stored in a knowledge graph formally describe a real situation with its entities and the relationships between these entities. In this context, the definition of a schema is based on one principle:

entities with the same nature have the same characteristics.

The schema thus expresses the expected semantic relationships between an entity and the rest of the represented universe, according to its nature. Consider as an example the description of a family by a knowledge graph.

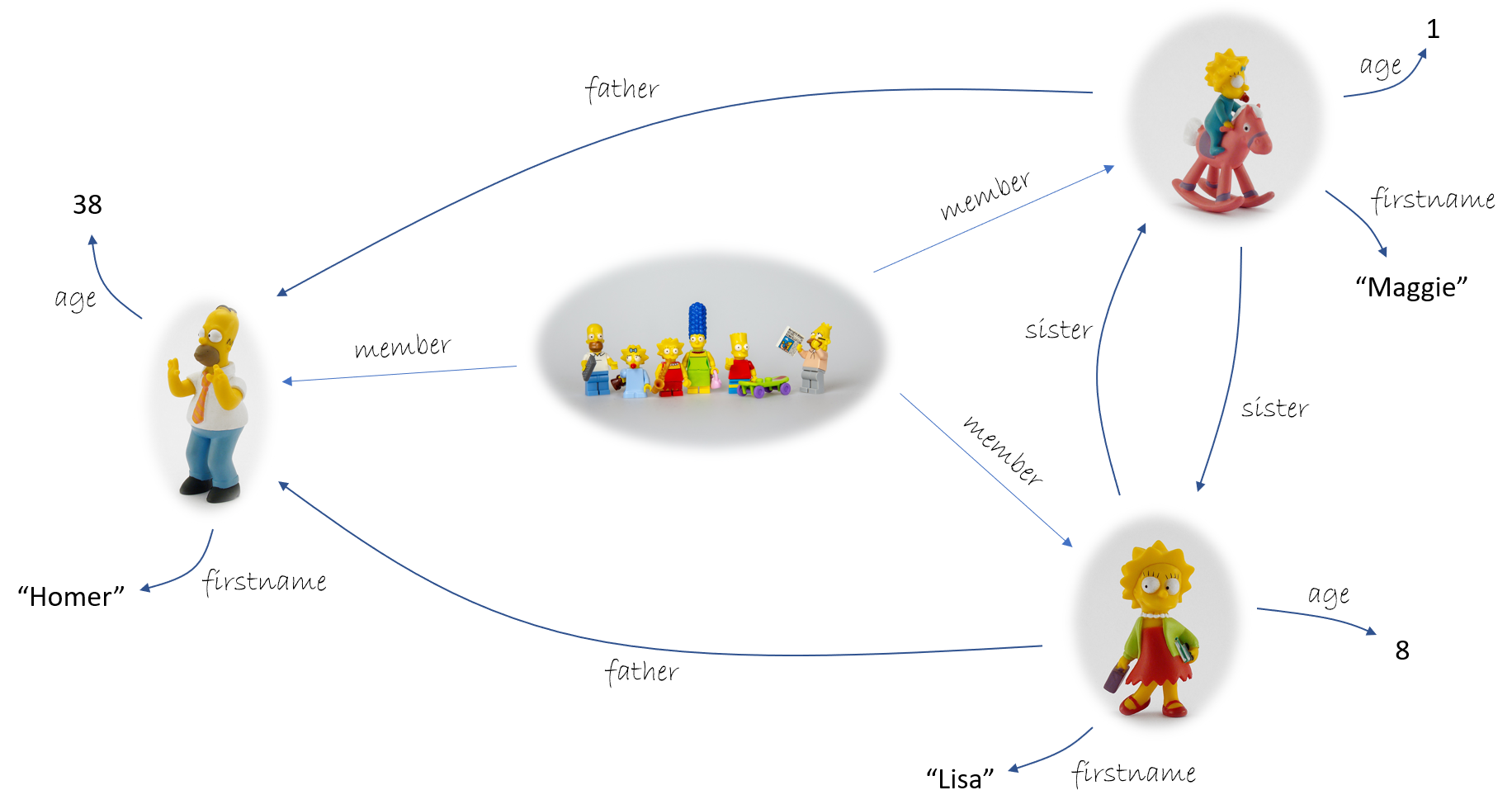
If we take the case of the member predicate edges in this graph, we would expect all triples of the form:

< ... member ... >

to refer homogeneously to the relationship between a family and a person belonging to that family. This is indeed the meaning conveyed by member. And this applies to all triples: each predicate (2nd position in the triple - see previous post) identifies a complete category of relations between subjects and objects (1st and 3rd positions in the triple).

The previous example focused on the edges of the graph, but the same principle applies to nodes. In the example, we can identify the category of all persons, noting that each element has a firstname and an age. Unlike the member example, which is already present in the knowledge graph, the terms family and person are not. To correct this, we add triples of the following form:

< lisa is_a Person >
< simpson is_a Family >
...

We note the use of the new (but very important) identifier is_a, which expresses belonging to a cateogy.

Giving the schema of knowledge graphs representing families, or more generally of a set of knowledge graphs, consists in enumerating all the node categories, predicates and construction constraints imposed by their semantics. This requires a syntax.

Writing a Schema

Since the schema summarizes a body of knowledge about the shape of the knowledge graphs we wish to manipulate, it can itself be described through... a knowledge graph! To illustrate this construction, let us start with the very special case of the is_a predicate above. As it allows us to translate the nature of the entity represented by a node, its object is a class of nodes (or type or concept depending on the tool, standard, ...). This gives us our first schema elements: Family and Person are classes. Translated in terms of triples, we get:

< Family is_a Class >
< Person is_a Class >

we note here the use of the is_a predicate again. From this point on, only the imagination can stop you from writing a schema! For example:

< Family is_a Class >
< Person is_a Class >
< Student is_a Class >
< Student subClassOf Person >
< firstname is_a DataProperty >
< firstname domain Person >
< firstname range string >
< Family is_a Class >
< member is_a ObjectProperty >
< member domain Person >
< member range Family >
< age is_a DataProperty >
< age is_a FunctionalProperty >
< age domain Person >
< age range integer >
...

Well, let's be honest, it's the imagination but above all the meaning we put behind all these new constructions (subClassOf, domain, range, etc.) that we want to be shared with as many people as possible. Indeed, where there's syntax, there's semantics. Let's take a quick look at some of the constructions we've used above, along with their meanings:

• Class, DataProperty and ObjectProperty: these schema nodes represent the concepts of class, data property and object property we've already discussed. They appear as objects of the is_a predicate (there it is again!): they are therefore classes. We can feel the need for a schema of schemas to ensure that a schema is itself well written. Here we enter to the world of meta-models and their ability to self-describe.

• domain and range specify the signatures of the predicates that will be used in the knowledge graphs under consideration, i.e. the classes to which the subjects and objects they link must respectively belong for their use to be valid. Thus, in our example, the subjects of firstname will be instances of the Person class, the objects of member will be instances of Family, and so on.

• subClassOf: specialization is a classic modeling construction that identifies the existence of a sub-category of instances within a class. In the example, it is specified that among the people there are students. The construction doesn't say more, but constraints specific to students can now be requested (e.g., the institution in which they are enrolled) in addition to those imposed on all persons.

• FunctionalProperty: this last construction constrains a predicate to apply only once to a given subject. Thus, we expect age to be a unique property for each person, otherwise it would be permissible to write: < maggy age 1 > and < maggy age 2 > which would make no sense in terms of the natural semantics of the age identifier.

There are many other conceivable constraints for creating a schema. The aim here is not to make an exhaustive list, but simply to convey their flavor, a flavor that for the moment remains rather informal. This is where standards really come into play; they provide the semantics of these constructs, i.e. their precise, mathematical meaning, so that anyone can correctly interpret the expectations encoded in a schema.

Some Standards

Standards are there to crystallize consensus on particular uses of knowledge graphs. To open up our discussion a little towards technologies, here are a few Semantic Web standards by the W3C dedicated to writing schemas for RDF graphs.

• RDF (for Resource Description Framework): The RDF standard not only defines a certain notion of knowledge graph, but also proposes a number of additional constructs, including the beginnings of a vocabulary. These include rdf:type (which we called is_a above) and rdf:Property (the predicate symbol class). RDF also offers constructs for manipulating sequences. Even so, these are still too limited to be called schemas.

• RDFS (for RDF Schema): This is a first minimal extension of the RDF vocabulary, which provides the basis for the elements introduced in this post, notably the notions of rdfs:class, rdfs:range, rdfs:domain, etc. Although very simple, most of the RDF vocabulary can be used as a schema. Although very simple, most RDF structure description languages are based on RDFS, which makes it a fundamental element of RDF-style Semantic Web tools.

• SHACL (for Shapes Constraint Language): This consequent extension of the RDFS vocabulary was designed to allow the specification of a set of constraints on the structure of RDF graphs. From this point of view, SHACL is fully in line with the notion of schema as described above. This language is based on the notion of shape, which describes an expectation of the form that a knowledge graph must locally respect. For example, we can express the FunctionalProperty construct seen above by requiring that any node of class Person has at most one outgoing edge labeled by the predicate age; in SHACL: < cstr_functional_age is_a PropertyShape > < cstr_functional_age targetClass Person > < cstr_functional_age path age > < cstr_functional_age maxCount 1 >.

• OWL (for Web Ontology Language): This further extension of RDFS provides the means to describe an RDF schema in the guise of an ontology, even if this is not its primary purpose. In fact, a (formal) ontology makes it possible to describe a domain of interest through the data of a set of knowledge ranging from its basic elements (individuals), their relationships, the description of these relationships, and so on. If we understand individuals and their relationships here as an RDF knowledge graph, the description of these relationships corresponds to a conceptualization of what is represented (identification of classes/concepts, properties and associated constraints). What sets OWL apart from RDF schema specification languages is that an ontology aims to describe the domain of interest, not the graphs representing the instances. Nevertheless, it is a fine boundary, and modeling a domain (through an ontology) is an excellent starting point for designing business tools (notably databases/knowledge) in an MBSE approach.

Conclusion

The primary characteristic of semi-structured data models is that they offer a representation mechanism for which schema is not a prerequisite. Their own structure is sufficient to organize the data. However, describing the way in which data is structured by means of a schema serves to validate it and make it usable by IT tools. We have seen that, in the case of knowledge graphs à la RDF, a schema comes quite naturally in the form of a typing system based on the identification of the membership of graph elements to certain categories. As far as RDF is concerned, there are various standards for specifying a schema (for different uses).

The standards presented offer a syntax for describing how to constrain the form of a class of knowledge graphs of interest. However, moving from the semantics of this syntax (sometimes given semi-formally or even informally) to an operational tool that actually checks whether the constraints are verified by a given graph is not a simple task. In the next few posts, we'll take a look at the world of logic rules and reasoning engines, which provide a solution to this question; we'll also see their interest in modeling and how they can link database and reasoning.

Antoine, scientific expert